Drittvariablenkontrolle in der Tabellenanalyse #

Durch verschiedene Maßzahlen können die Werte einer Kreuztabelle analysiert werden. Es kann auch der Einfluss einer Drittvariablen überprüft werden. Diese werden mit Z bezeichnet. Z kann die Beziehung von X und Y beeinflussen oder auch nicht. Liegt eine Beeinflussung vor, kann das in verschiedenen Konstellationen passieren. Einige dieser Konstellationen werden dir im Folgenden in modellhafter Form vorgestellt: das Modell der gemeinsamen Ursache, das Interventionsmodell, das Interaktionsmodell und das additive Kausalmodell.

Die Unterscheidung der Modelle ist in der Regel auf Grundlage der Betrachtung der Prozentsatzdifferenzen und der Spaltenprozentsätze möglich. Einige Modelle können nur theoretisch unterschieden werden.

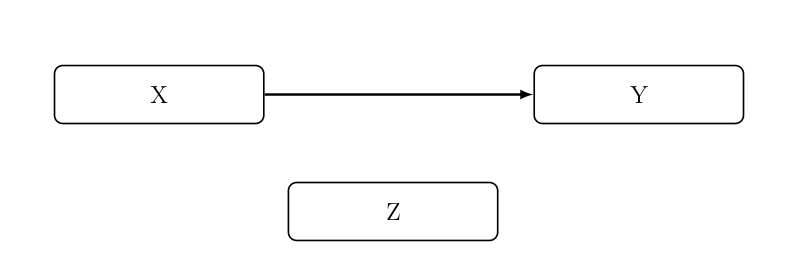
Kein Einfluss der Drittvariablen #

Wenn die Spaltenprozentsätze der Partialtabellen denen der Marginaltabelle entsprechen und die Prozentsatzdifferenz gleich bleibt, beeinflusst die Drittvariable Z die Beziehung von X und Y nicht. Die möglicherweise festgestellte Korrelation wird durch die Drittvariable, zumindest durch diese, nicht aufgehoben. Die Drittvariable Z hat keine Einfluss auf X oder Y.

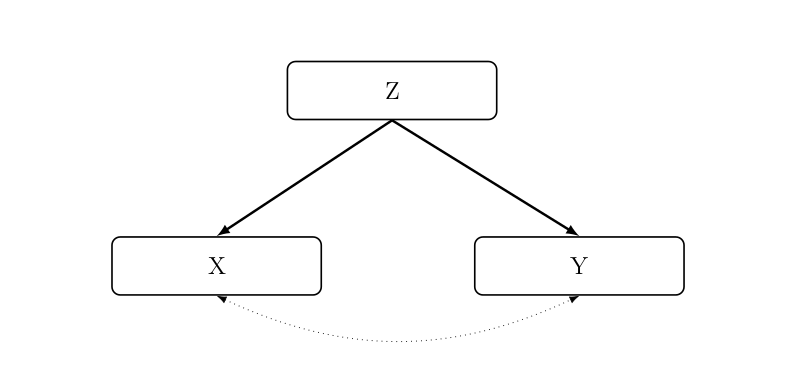
Modell der gemeinsamen Ursache #

Beim Modell der gemeinsamen Ursache lässt Z den augenscheinlichen Zusammenhang zwischen der unabhängigen Variable X und der abhängigen Variable Y verschwinden. Gab es vor der Kontrolle Z vielleicht signifikante Korrelationen, werden diese aufgelöst, weil Z die gemeinsame Ursache sowohl von X als auch Y ist. X und Y selbst hängen gar nicht miteinander zusammen. Modell der gemeinsamen Ursache: Z hebt den Zusammenhang zwischen X und Y auf. Z beeinflusst sowohl X als auch Y.

Interventionsmodell #

Das Interventionsmodell zeigt die selben Anzeichen wie das Modell der gemeinsamen Ursache: Der Zusammenhang zwischen X und Y verschwindet. Allerdings beeinflusst Z nicht X und Y, sondern liegt zwischen den beiden originären Variablen. Es vermittelt folglich den Einfluss von X auf Y. Interventionsmodell: Z hebt den Zusammenhang zwischen X und Y auf. Z vermittelt den Einfluss von X auf Y.

Das Modell der gemeinsamen Ursache sowie das Interventionsmodell sind von den statistischen Ergebnissen her nicht voneinander zu unterscheiden. Das Verhältnis von Prozentsatzdifferenzen und Spaltenprozentsätzen sind gleich. Eine Unterscheidung ist daher nur auf theoretischer Basis möglich.

Interaktionsmodell #

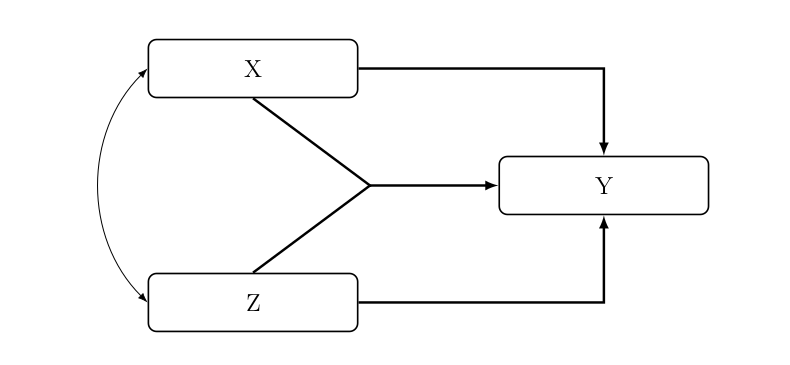
Interagieren X und Z bei der Erklärung von Y, liegt ein Interaktionseffekt vor. X und Z haben in diesem Fall eine bivariaten Zusammenhang.

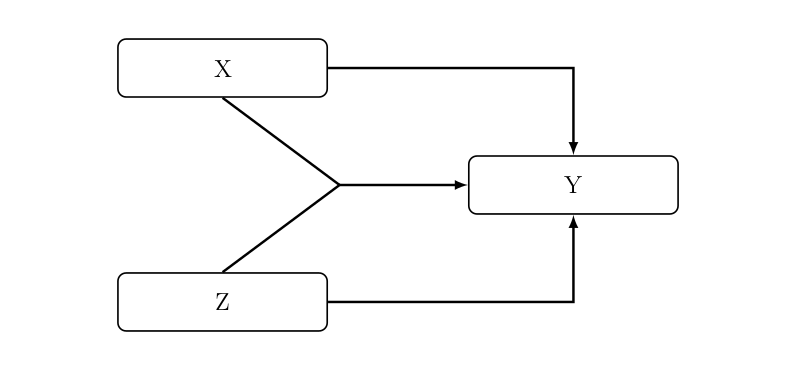
X und Z können dabei untereinander korrelieren, müssen es aber nicht. Interaktionsmodell mit Korrelation: X und Z interagieren bei der Erklärung von Y und korrelieren dabei. Interaktionsmodell ohne Korrelation: X und Z interagieren bei der Erklärung von Y, aber korrelieren nicht.

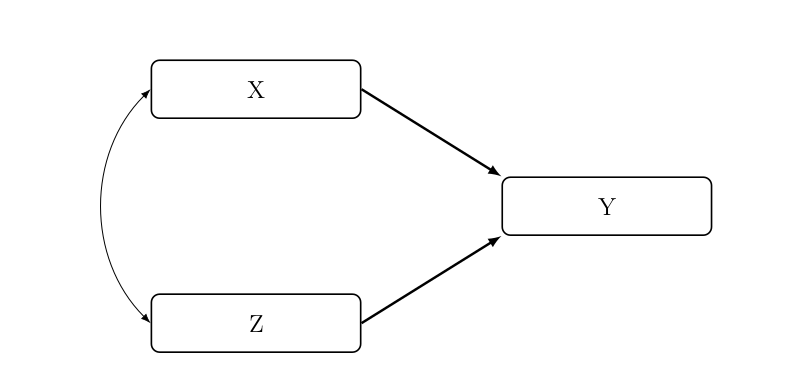
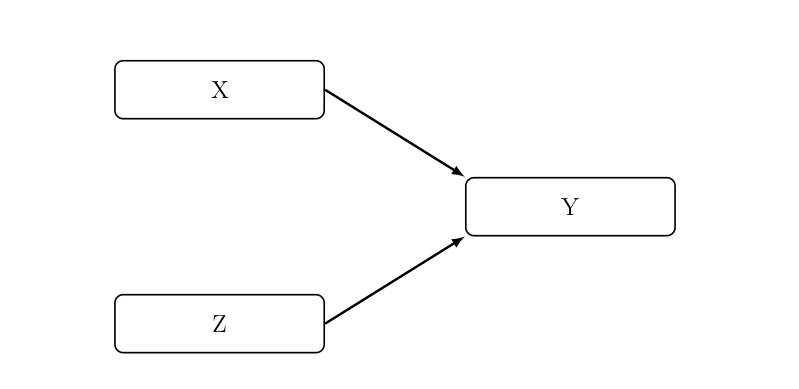
Additives Kausalmodell #

Bei einer additiven Kausalität beeinflussen sowohl X als auch Z Y. Die Einflüsse auf Y sind unabhängig voneinander. Die Prozentsatzdifferenz der Partialtabellen ist gleich und größer als 0, die Niveaus der Spaltenprozentsätze ändern sich. X und Z können dabei korrelieren oder nicht. Additives Kausalmodell mit Korrelation: Ohne miteinander zu interagieren, beeinflussen sowohl X als auch Z Y. Dabei korrelieren sie nicht.